Si es un profesional de SEO o un especialista en marketing digital y lee este artículo, es posible que haya experimentado con IA y chatbots en su trabajo diario.
Pero la pregunta es: ¿cómo se puede aprovechar al máximo la IA además de utilizar una interfaz de usuario de chatbot?
Para ello, necesita una comprensión profunda de cómo funcionan los modelos de lenguaje grandes (LLM) y aprender el nivel básico de codificación. Y sí, la codificación es absolutamente necesaria para tener éxito como profesional de SEO hoy en día.
Este es el primero de una serie de artículos que tienen como objetivo mejorar sus habilidades para que pueda comenzar a utilizar LLM para escalar sus tareas de SEO. Creemos que en el futuro, esta habilidad será necesaria para tener éxito.
Necesitamos empezar desde lo básico. Incluirá información esencial, por lo que más adelante en esta serie podrá utilizar los LLM para escalar sus esfuerzos de SEO o marketing para las tareas más tediosas.
A diferencia de otros artículos similares que haya leído, comenzaremos aquí desde el final. El siguiente vídeo ilustra lo que podrá hacer después de leer todos los artículos de la serie sobre cómo utilizar los LLM para SEO.
Nuestro equipo utiliza esta herramienta para agilizar los enlaces internos manteniendo la supervisión humana.
¿Te gustó? Esto es lo que podrás construir tú mismo muy pronto.
Ahora, comencemos con lo básico y le proporcionemos los conocimientos previos necesarios en LLM.
¿Qué son los vectores?
En matemáticas, los vectores son objetos descritos por una lista ordenada de números (componentes) correspondientes a las coordenadas en el espacio vectorial.
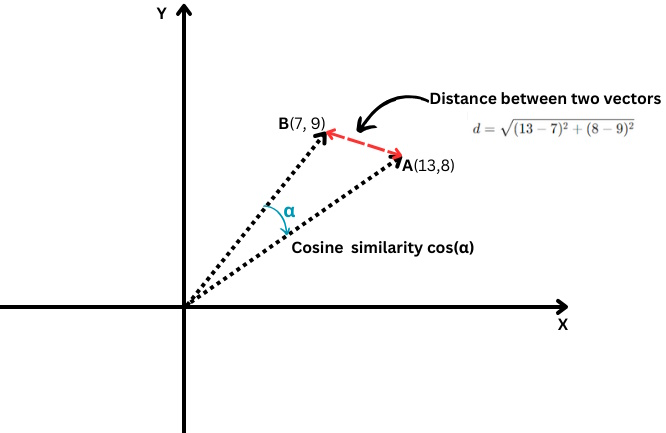
Un ejemplo simple de vector es un vector en un espacio bidimensional, que está representado por (x,y) coordenadas como se ilustra a continuación.
En este caso, la coordenada x=13 representa la longitud de la proyección del vector en el eje X, y y=8 representa la longitud de la proyección del vector en el eje Y.
Los vectores que se definen con coordenadas tienen una longitud, que se llama magnitud de un vector o norma. Para nuestro caso simplificado bidimensional, se calcula mediante la fórmula:
Sin embargo, los matemáticos siguieron adelante y definieron vectores con un número arbitrario de coordenadas abstractas (X1, X2, X3… Xn), lo que se denomina vector “N-dimensional”.
En el caso de un vector en el espacio tridimensional, serían tres números (x,y,z), que aún podemos interpretar y comprender, pero cualquier cosa por encima de eso está fuera de nuestra imaginación, y todo se convierte en un concepto abstracto.
Y aquí es donde entran en juego las incorporaciones de LLM.
¿Qué es la incrustación de texto?
Las incrustaciones de texto son un subconjunto de incrustaciones LLM, que son vectores abstractos de alta dimensión que representan texto y capturan contextos semánticos y relaciones entre palabras.
En la jerga de LLM, las «palabras» se denominan tokens de datos y cada palabra es un token. De manera más abstracta, las incrustaciones son representaciones numéricas de esos tokens, que codifican relaciones entre cualquier token de datos (unidades de datos), donde un token de datos puede ser una imagen, una grabación de sonido, un texto o un cuadro de video.
Para calcular qué tan cercanas están semánticamente las palabras, necesitamos convertirlas en números. Así como restas números (por ejemplo, 10-6=4) y puedes saber que la distancia entre 10 y 6 es 4 puntos, es posible restar vectores y calcular qué tan cerca están los dos vectores.
Por lo tanto, comprender las distancias vectoriales es importante para comprender cómo funcionan los LLM.
Hay diferentes formas de medir qué tan cerca están los vectores:
- Distancia euclidiana.
- Semejanza o distancia del coseno.
- Similitud con Jaccard.
- Distancia de Manhattan.
Cada uno tiene sus propios casos de uso, pero discutiremos solo las distancias euclidianas y cosenos de uso común.
¿Qué es la similitud del coseno?
Mide el coseno del ángulo entre dos vectores, es decir, qué tan cerca están alineados esos dos vectores entre sí.
Distancia euclidiana versus similitud del cosenoSe define de la siguiente manera:
Donde el producto escalar de dos vectores se divide por el producto de sus magnitudes, también conocidas como longitudes.
Sus valores van desde -1, que significa completamente opuesto, hasta 1, que significa idéntico. Un valor de ‘0’ significa que los vectores son perpendiculares.
En términos de incrustaciones de texto, es poco probable lograr el valor exacto de similitud de coseno de -1, pero aquí hay ejemplos de textos con 0 o 1 similitudes de coseno.
Similitud del coseno = 1 (idéntico)
- “Las 10 mejores joyas escondidas para viajeros solitarios en San Francisco”
- “Las 10 mejores joyas escondidas para viajeros solitarios en San Francisco”
Estos textos son idénticos, por lo que sus incrustaciones serían las mismas, lo que daría como resultado una similitud coseno de 1.
Similitud del coseno = 0 (perpendicular, lo que significa no relacionado)
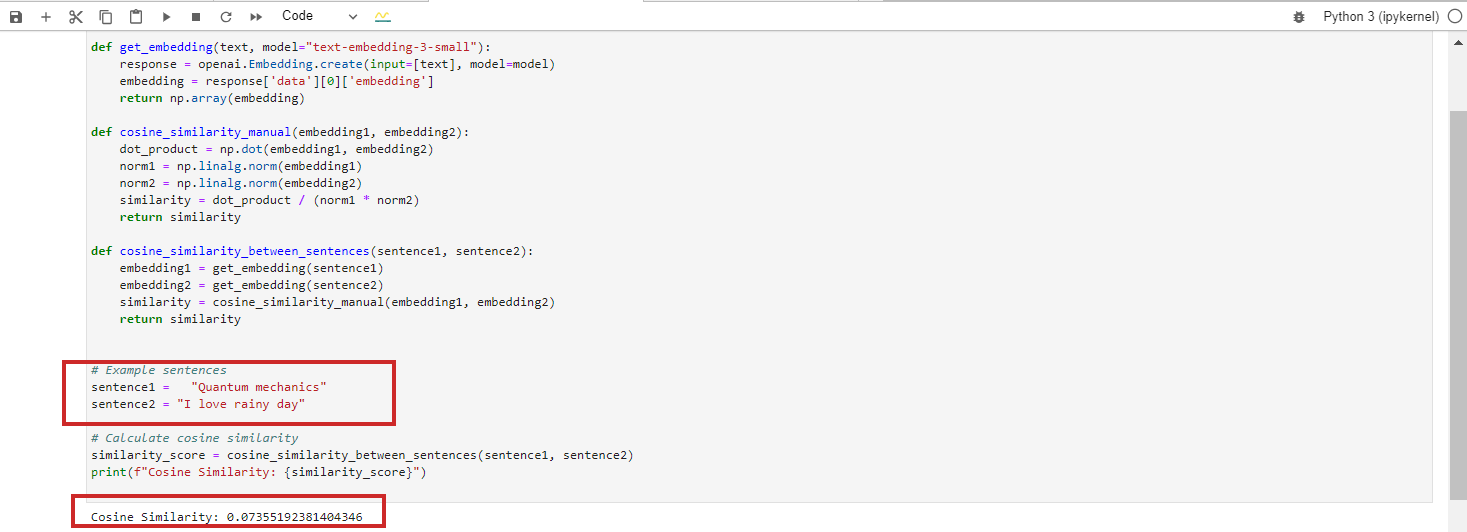
- «Mecánica cuántica»
- “Me encantan los días lluviosos”
Estos textos no tienen ninguna relación, lo que da como resultado una similitud de coseno de 0 entre sus incorporaciones BERT.
Sin embargo, si ejecuta el modelo de incrustación de Google Vertex AI ‘text-embedding-preview-0409’, obtendrá 0,3. Con los modelos ‘text-embedding-3-large’ de OpenAi, obtendrás 0,017.
(Nota: aprenderemos en detalle en los próximos capítulos practicando con incrustaciones usando Python y Jupyter).
Modelo de texto-‘incrustación-preview-0409′ de Vertex Ai
Modelo de ‘incrustación de texto-3-pequeño’ de OpenAi
Nos saltamos el caso con similitud de coseno = -1 porque es muy poco probable que suceda.
Si intenta obtener similitud de coseno para texto con significados opuestos como «amor» frente a «odio» o «el proyecto exitoso» frente a «el proyecto fallido», obtendrá una similitud de coseno de 0,5-0,6 con el texto de Google Vertex AI. modelo de incrustación-preview-0409′.
Esto se debe a que las palabras «amor» y «odio» a menudo aparecen en contextos similares relacionados con las emociones, y «exitoso» y «fracaso» están relacionados con los resultados del proyecto. Los contextos en los que se utilizan pueden superponerse significativamente en los datos de entrenamiento.
La similitud del coseno se puede utilizar para las siguientes tareas de SEO:
- Clasificación.
- Agrupación de palabras clave.
- Implementación de redirecciones.
- Vinculación interna.
- Detección de contenido duplicado.
- Recomendación de contenido.
- Análisis de la competencia.
La similitud del coseno se centra en la dirección de los vectores (el ángulo entre ellos) en lugar de su magnitud (longitud). Como resultado, puede capturar similitudes semánticas y determinar qué tan cerca se alinean dos contenidos, incluso si uno es mucho más largo o usa más palabras que el otro.
Profundizar y explorar cada uno de estos será el objetivo de los próximos artículos que publicaremos.
¿Qué es la distancia euclidiana?
En caso de que tenga dos vectores A(X1,Y1) y B(X2,Y2), la distancia euclidiana se calcula mediante la siguiente fórmula:
Es como usar una regla para medir la distancia entre dos puntos (la línea roja en el cuadro de arriba).
La distancia euclidiana se puede utilizar para las siguientes tareas de SEO:
- Evaluar la densidad de palabras clave en el contenido.
- Encontrar contenido duplicado con una estructura similar.
- Análisis de la distribución del texto de anclaje.
- Agrupación de palabras clave.
A continuación se muestra un ejemplo de cálculo de distancia euclidiana con un valor de 0,08, casi cercano a 0, para contenido duplicado donde los párrafos simplemente se intercambian, lo que significa que la distancia es 0, es decir, el contenido que comparamos es el mismo.
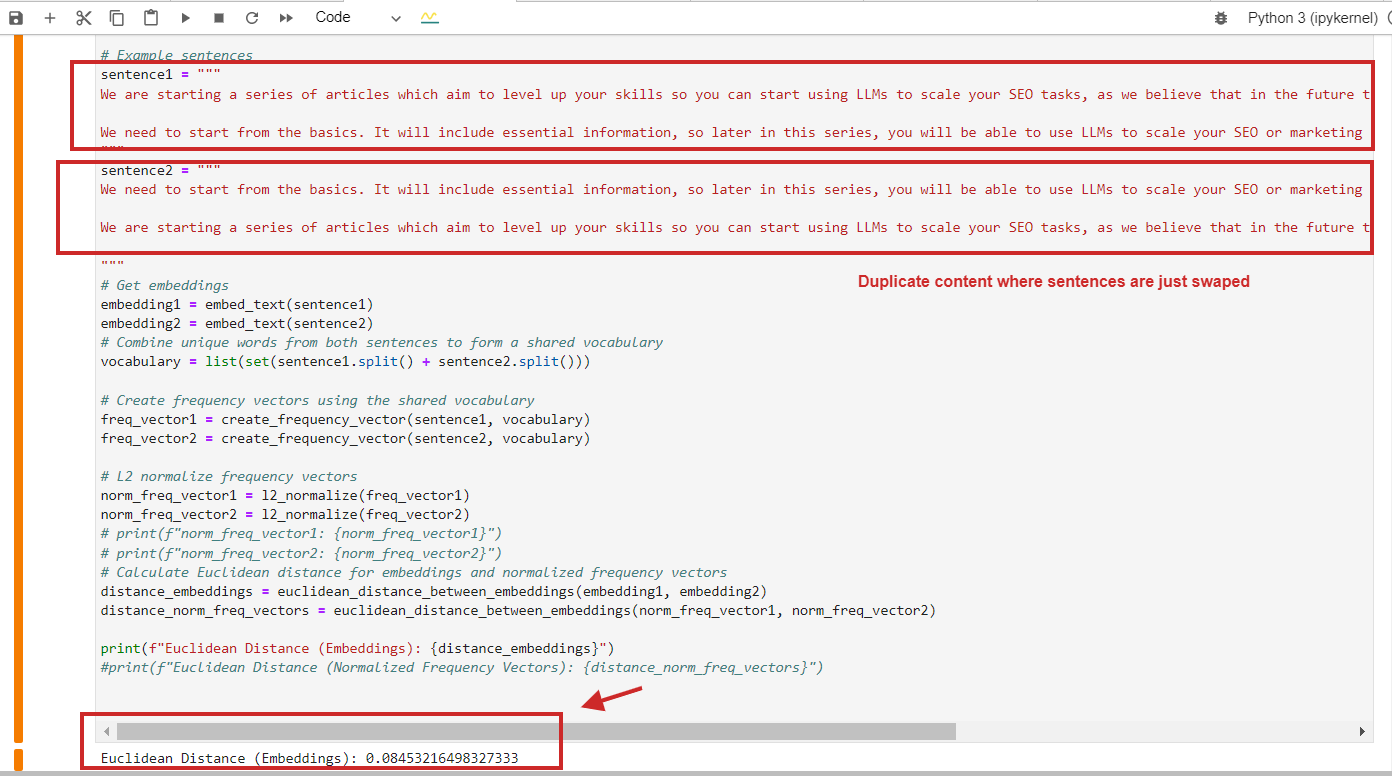Ejemplo de cálculo de distancia euclidiana de contenido duplicadoPor supuesto, puede utilizar la similitud del coseno y detectará contenido duplicado con una similitud del coseno de 0,9 sobre 1 (casi idéntico).
Aquí hay un punto clave para recordar: no debe confiar simplemente en la similitud del coseno, sino también utilizar otros métodos, ya que el artículo de investigación de Netflix sugiere que el uso de la similitud del coseno puede conducir a «similitudes» sin sentido.
Mostramos que la similitud coseno de las incorporaciones aprendidas puede, de hecho, producir resultados arbitrarios. Descubrimos que la razón subyacente no es la similitud coseno en sí, sino el hecho de que las incorporaciones aprendidas tienen un grado de libertad que puede generar similitudes cosenos arbitrarias.
Como profesional de SEO, no es necesario que pueda comprender completamente ese documento, pero recuerde que las investigaciones muestran que se deben considerar otros métodos a distancia, como el euclidiano, en función de las necesidades del proyecto y el resultado que se obtenga para reducir las falsas expectativas. resultados positivos.
¿Qué es la normalización L2?
La normalización L2 es una transformación matemática aplicada a vectores para convertirlos en vectores unitarios con una longitud de 1.
Para explicarlo en términos simples, digamos que Bob y Alice caminaron una larga distancia. Ahora queremos comparar sus direcciones. ¿Siguieron caminos similares o tomaron direcciones completamente diferentes?
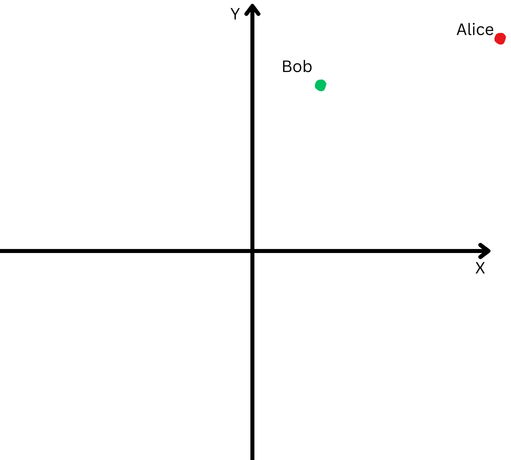«Alice» está representada por un punto rojo en el cuadrante superior derecho y «Bob» está representado por un punto verde.Sin embargo, como están lejos de su origen, tendremos dificultades para medir el ángulo entre sus trayectorias porque han ido demasiado lejos.
Por otro lado, no podemos afirmar que si están lejos uno del otro significa que sus caminos son diferentes.
La normalización L2 es como llevar a Alice y Bob a la misma distancia más cercana desde el punto de partida, digamos a un pie del origen, para que sea más fácil medir el ángulo entre sus trayectorias.
Ahora vemos que, aunque están muy separados, las direcciones de sus trayectorias son bastante cercanas.
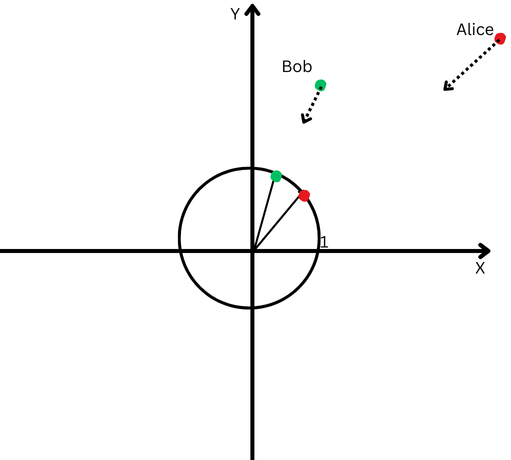Un plano cartesiano con un círculo centrado en el origen.Esto significa que hemos eliminado el efecto de sus diferentes longitudes de trayectoria (también conocidas como magnitud de vectores) y podemos centrarnos exclusivamente en la dirección de sus movimientos.
En el contexto de las incrustaciones de texto, esta normalización nos ayuda a centrarnos en la similitud semántica entre textos (la dirección de los vectores).
La mayoría de los modelos de incrustación, como los modelos ‘text-embedding-3-large’ de OpeanAI o ‘text-embedding-preview-0409’ de Google Vertex AI, devuelven incrustaciones prenormalizadas, lo que significa que no es necesario normalizar.
Pero, por ejemplo, las incorporaciones ‘bert-base-uncased’ del modelo BERT no están prenormalizadas.
Conclusión
Este fue el capítulo introductorio de nuestra serie de artículos para familiarizarlo con la jerga de los LLM, que espero que haya hecho que la información sea accesible sin necesidad de un doctorado en matemáticas.
Si todavía tienes problemas para memorizarlos, no te preocupes. A medida que cubrimos las siguientes secciones, nos referiremos a las definiciones definidas aquí y usted podrá comprenderlas a través de la práctica.
Los próximos capítulos serán aún más interesantes:
- Introducción a las incrustaciones de texto de OpenAI con ejemplos.
- Introducción a las incrustaciones de texto Vertex AI de Google con ejemplos.
- Introducción a las bases de datos vectoriales.
- Cómo utilizar incrustaciones de LLM para enlaces internos.
- Cómo utilizar incrustaciones de LLM para implementar redirecciones a escala.
- Poniéndolo todo junto: complemento de WordPress basado en LLM para enlaces internos.
El objetivo es mejorar tus habilidades y prepararte para enfrentar desafíos en SEO.
Muchos de ustedes pueden decir que hay herramientas que pueden comprar y que hacen este tipo de cosas automáticamente, pero esas herramientas no podrán realizar muchas tareas específicas según las necesidades de su proyecto, que requieren un enfoque personalizado.
Usar herramientas de SEO siempre es genial, ¡pero tener habilidades es aún mejor!
Más recursos:
Imagen destacada: Krot_Studio/Shutterstock
